Koordinatendarstellung Koordinaten von Vektoren
Ganz allgemein kann ein beliebiger ebener Vektor so verschoben werden, dass der Anfang des Pfeiles im Koordinatenursprung liegt. Dadurch erhalten wir ganz allgemein für ebene Vektoren eine Koordinatendarstellung:
Merke:
Um die Koordinaten eines beliebigen Vektors \(\overrightarrow{v}\) zu bestimmen, verschieben wir ihn so, dass sein Ursprung mit dem Koordinatenursprung \((0\,|\,0)\) übereinstimmt. Ist dann \(P = (x \, \vert \, y)\) der Endpunkt des Vektorpfeiles, so ist
\(\qquad\overrightarrow{v} = \left( \begin{matrix} x \\ y \end{matrix} \right)\)
die Koordinatendarstellung von \(\overrightarrow{v}\).
Die Koordinatendarstellung eines Verbindungsvektors von zwei Punkten \(P\) und \(Q\) kann sehr leicht aus den Koordinaten der Punkte \(P\) und \(Q\) bestimmt werden.
Beispiel:
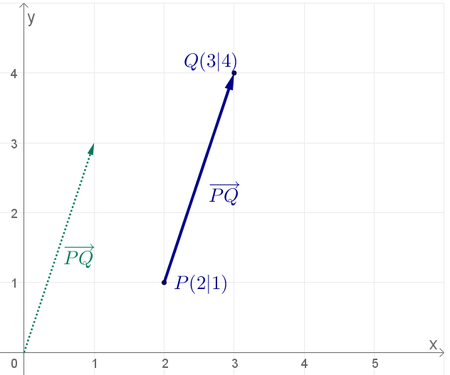
Betrachten wir etwa den Verbindungsvektor \(\overrightarrow{PQ}\) der beiden Punkte \(P = (2 \, \vert \, 1)\) und \(Q = (3 \, \vert \, 4)\), und verschieben wir diesen Vektor so, dass sein Ursprung im Koordinatenursprung liegt, so hat der Endpunkt die Koordinaten \((1 \, \vert \, 3)\), wir haben also
\(\qquad\overrightarrow{PQ} = \left( \begin{matrix} 1 \\ 3 \end{matrix} \right)\)
Ganz allgemein gilt:
Merke:
Der Verbindungsvektor \(\overrightarrow{PQ}\) der beiden Punkte \(P = (p_1 \, \vert \, p_2)\) und \(Q = (q_1 \, \vert \, q_2)\) hat die Koordinatendarstellung
\(\qquad\overrightarrow{PQ} = \left( \begin{matrix} q_1 -p_1 \\ q_2 - p_2 \end{matrix} \right)\)
Mit der Koordinatendarstellung kann die Gleichheit von zwei Vektoren sehr viel einfacher überprüft werden als mit der geometrischen Darstellung:
Merke:
Zwei Vektoren \(\overrightarrow{v} = \left( \begin{matrix} v_1 \\ v_2 \end{matrix} \right)\) und \(\overrightarrow{w} = \left( \begin{matrix} w_1 \\ w_2 \end{matrix} \right)\) sind genau dann gleich, wenn \(w_1 = v_1\) und \(w_2 = v_2\).
\(\enspace\)